| [5ème/4è] Le théorème de Pythagore |
| « Citoyen » Membre 1483125840000
| 0 | ||
| Le Théorème de Pythagore Voici le théorème de Pythagore, nous allons voir son énoncé, et sa démonstration Notions préliminaires Vous pouvez sauter cette partie si vous êtes à l'aise avec les notions de base ou si vous êtes en 3è ou +. Il y a quelques notions à connaître d'abord avant de connaître le théorème. D'abord, il faut savoir ce qu'est l'hypoténuse d'un triangle rectangle. Il est utile de rappeler qu'un triangle rectangle est un polygone à trois côtés avec un angle droit (de 90°). L'hypoténuse d'un triangle rectangle est donc le côté opposé à l'angle droit. Ici, l'hypoténuse du triangle ABC est le segment [AC]. J'insiste sur le fait que l'hypoténuse est un segment, il est faux de dire que AC est l'hypoténuse du triangle ABC, c'est [AC], par les conventions de notations en géométrie.  Ensuite, il faut introduire les notions de carré d'un nombre et de racine carrée Lorsque l'on parle de carré d'un nombre, ce n'est pas la figure géométrique du carré, mais cela a un rapport avec celle ci. Rappelons que l'aire d'un carré est égale à la longueur de son côté multiplié par cette même longueur, qui, plus rapidement, est égale au côté au carré.   Le carré d'un nombre est donc le produit de ce nombre par ce nombre, c'est la multiplication d'un nombre par lui-même. c² = c × c Donc voici la table des carrés pour ceux qui seraient intéressés. Table des carrés 0² = 0 × 0 = 0 1² = 1 × 1 = 1 2² = 2 × 2 = 4 3² = 3 × 3 = 9 4² = 4 × 4 = 16 5² = 5 × 5 = 25 6² = 6 × 6 = 36 7² = 7 × 7 = 49 8² = 8 × 8 = 64 9² = 9 × 9 = 81 10² = 10 × 10 = 100 11² = 11 × 11 = 121 12² = 12 × 12 = 144 13² = 13 × 13 = 169 14² = 14 × 14 = 196 15² = 15 × 15 = 225 16² = 16 × 16 = 256 17² = 17 × 17 = 289 18² = 18 × 18 = 324 19² = 19 × 19 = 361 20² = 20 × 20 = 400 Maintenant, il faut aussi connaître la notion de racine carrée, en fait, cette notion est très difficile à expliquer pour ceux qui voient cette notion pour la première fois. Par, exemple, quelle est la longueur du côté d'un carré dont l'aire vaut 9 cm² (je rappelle que lorsque l'on parle d'aire, on parle pas de centimètres mais de centimètres carrés), et si l'aire du carré était de 81 cm², et si l'aire du carré était de 324 cm² ? Si vous avez vu la table des carrés, les réponses à cette question sont respectivement 3 cm, 9 cm et 18 cm. En fait, on dit que 3 est la racine carrée de 9, que 9 est la racine carrée de 81 et que 18 est la racine carrée de 324. Question plus difficile : Et si le carré avait pour aire 30 cm² ? La réponse est la racine carrée de 30. En fait, en mathématiques, lorsque l'on demande une valeur exacte, c'est une valeur exacte qu'il faut mettre et non une valeur approchée. La racine carrée de 30 est donc une valeur exacte, contrairement à son approximation de 5.477 . La racine carré d'un nombre est le nombre tel que le carré de ce nombre vaut le nombre initial. Cette définition est juste, mais imprécise. Il faut une réponse plus précise. La racine carrée b d'un nombre a est le nombre b tel que b × b = a. Et ça c'est valable quelque soit le nombre a. On dit que b = √(a), en fait, normalement il y a pas besoin de parenthèses, mais l'informatique ne nous permet pas d'écrire comme on voudrait. En informatique par exemple, dans un des codes de mathématiques, on dit que b = sqrt(a) Si vous écrivez à la main ou sur une feuille de papier, vous devrez écrire ça :  Si la racine carrée vous semble trop abstrait, je vous invite à relire ce qui est écrit ci-dessus car nous allons attaquer le gros morceau. Le théorème Voici l'énoncé du théorème. Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Voici le théorème en illustration AC² = AB² + BC² ou si vous voulez , AC × AC = AB × AB + BC × BC  Ou encore, l'aire du carré rouge est égale à la somme de l'aire du carré bleu et de l'aire du carré vert. Nous verrons les utilités du théorème après. La démonstration Avant de démontrer le théorème je recommande pour ceux qui n'ont pas déjà vu ou fait la démonstration d'essayer de le faire eux-même, en tout cas pour ceux qui sont en 3è ou plus. Nous allons démontrer le théorème. En fait, nous allons démontrer le théorème pour tous les triangles rectangles. D'abord, il faut savoir que l'aire d'un triangle est égale au produit des longueurs de ses côtés droits divisé par deux (les côtés qui se coupent sur l'angle droit grossièrement) Ici, (AB x BC)/ 2 (le slash correspond à la division) = AireABC  Attaquons la démonstration. On va supposer un triangle rectangle ABC rectangle en B. Maintenant, on va copier coller ce triangle de manière à obtenir ceci.  Même si j'ai la flemme de le démontrer, on se met d'accord sur le fait que le quadrilatère blanc est un carré. La longueur de son côté est égale à AC. Donc, L'espace blanc à l'intérieur du carré bleu est égale à AC². On va déplacer de nouveau les triangles rouges jusqu'à obtenir ceci :  De plus, les quadrilatères blancs formés sont toujours des carrés. L'aire du plus petit est de AB², pas trop dur de s'en convaincre. L'aire du plus grand est de AD², car j'ai rajouté un nouveau sommet D. Cependant, comme deux triangles rouges ABC de cette manière forment un rectangle, AD = BC et donc AD² = BC². L'espace blanc est de AB² + BC². Et comme l' "espace rouge" occupé est toujours la même, alors l'espace blanche occupée ne change pas. Cela nous conduit à l'égalité : AB² + BC² = AC². Cette méthode fonctionne pour tous les triangles rectangles, et donc on peut répéter cette opération autant de fois qu'il y a de triangles rectangles différents (je vous le déconseille car il y en a une infinité...) Il y a d'autres démonstrations, mais je trouve que celle-ci est la plus simple. Peut être que je vous en mettrai dans le post ci dessous. En fait, on peut démontrer ce théorème en une seule animation....  Donnez votre avis, ce que ce vous avez appris etc... J'espère que ce post vous sera utile. Dernière modification le 1483178700000 |
| « Citoyen » Membre 1483136160000
| 0 | ||
| Historique du théorème de Pythagore Le théorème de Pythagore a été formulé bien avant l'apparition du mathématicien grec. Les Babyloniens l'avaient déjà énoncé, il s'agit d'une hypothèse qui tient la route. Pythagore est en réalité un mathématicien plutôt méconnu. On sait seulement qu'il a vécu au VIè siècle de notre ère. Le premier ayant démontré ce théorème (ou plutôt, le premier dont on dispose des traces de la démonstration) est Euclide, dont je parlerais probablement dans un autre topic. Histoire de la racine carrée de 2 Si l'on prend un carré de côté 1, avec le théorème de Pythagore, on peut calculer que la longueur de la diagonale est égale à la racine carrée de 2. En fait, le problème, c'est que ce nombre est irrationnel, c'est à dire qu'il ne peut pas s'exprimer comme une fraction de deux entiers. Il vaut environ 1,41. Nous allons le prouver dans un autre topic (ici). Les Pythagoriciens eux, pensaient que tout nombre était rationnel, c'est à dire que tout nombre est une fraction de deux entiers. Cela a eu pour conséquences que l'un des disciples de Pythagore, ayant révélé l'irrationalité de ce nombre, a été noyé par son propre maître, enfin, selon la légende... Exemple d'application du théorème Prenons notre brave triangle ABC. 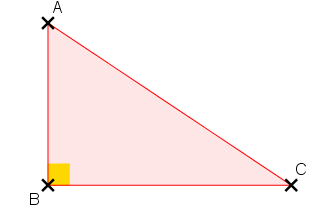 Appliquons lui le théorème de Pythagore puisqu'il est rectangle. Ainsi, AC² = AB²+ BC² d'après le théorème. On veut calculer AC. D'après le premier post, la racine carrée de AC² est égale à AC. 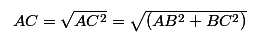 Ici, on a remplacé AC par AB²+BC² car AC = AB²+BC². Comme ces valeurs sont égales, on dit qu'on les substitue. Donc, au final, on a la jolie formule : 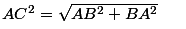 Si vous n'avez pas compris je reparlerais de substitution dans d'autres topics. En revanche, si vous avez compris, je vous invite à prouver ces deux autres égalités sur le même triangle : 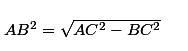 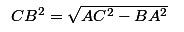 Dernière modification le 1483191540000 |
| « Consul » Membre 1484309580000
| 0 | ||
| Génial ! (même si y a moyen de faire plus simple) |
| « Censeur » Membre 1488137760000
| 0 | ||
| pas mal la démonstration je savais pas qu'on pouvait le faire sans le produit scalaire ^^ |
| « Censeur » Membre 1490724900000
| 0 | ||
| Ah merci j'avais oublié mais qu'est ce que ça date le théorème de Pythagore sans me vanter je l'ai appris a mes 9-10 ans grâce à mon frère bref je te remercie... |



























 Atelier 801
Atelier 801 Science4Mice
Science4Mice  Public
Public  Expositions publiques
Expositions publiques  Survoltaje
Survoltaje