| [Soutien scolaire] Aide aux devoirs |
| 1 | ||
| "for help" Ça pique |
| « Censeur » 1543352880000
| 1 | ||
Tenskk a dit : What kind of help do you need ? :)) |
| « Censeur » 1543654620000
| 0 | ||
Woowy a dit : Sauf que c'est correctement écrit "to help" ça aurait été "pour aider", là c'est "pour de l'aide" |
| 1 | ||
Devilyomita a dit : non là c'est "pour l'aide" pour de l'aide ce serait plus "for some help" |
| 0 | ||
| Coucou qui peut m'expliquer comment on place des fractions sur une droite graduée les amis, j'ai trouvé un exercice sur internet que je ne réussie pas et si vous pouviez me montrer comment vous avez complétez les exercices ça m'aiderait énormément à comprendre cela, milles remerciements ! Les exercices |
| « Censeur » 1543767300000
| 1 | ||
| tu regardes le nombre de barres séparant le 0 du 1. Sur l'exercice 1, il y a 6 barres. les fractions devront donc avoir un dénominateur en 6. si ce n'est pas le cas, il te suffira de mettre la fraction sur 6 Ensuite tu vois les fractions que tu dois placer : 1/2 , 1/3 , 5/6, 6/6 tu peux déjà placer le 6/6 qui correspond à 1. pour placer 5/6, tu n'as cas compter du nombre 0 à 1. (tu comptes 5 barres et ça arrive juste avant le 6/6) pour placer 1/3, c'est facile mais il te demande juste de la réflexion car la droite est partagée en 6 et non en 3 ! tu dois alors mettre au dénominateur 6 il suffit juste de mettre 1/3 sur x/6 tu fais alors 1 x 2 = 2 3 x 2 = 6 et puis là, tu peux placer 2/6 sur ta droite ! tu fais la même chose pour 1/2 1/2 = 3/6 j'ai essayé de faire une explication vraiment simple Dernière modification le 1543767660000 |
| 0 | ||
| Bonsoirrrrrrrrrrrrr ! Merci énormément Plantepur ! Juste le dernier exercice (le 2 donc) de ce site : Clique !!! et bah j'ai pas réussi, je me suis même fait une petite illustration pour m'aider et après quand je valide y'a écrit 'Une ou plusieurs erreurs, blabla", pouvez-vous essayer de le compléter et voir si vous avez eu TOUT BON (un message du genre "Bravo blabla apparaît", rip je sais que vous n'êtes pas des segpas), vraiment demain j'ai une éval et cet exercice m'aide beaucoup (les points (lettres) sont un peu décalés mais bon vous avez juste à les remettre en place c'est pas un problème), je vous montre ce que j'ai mis :-(, merci, j'ai vraiment besoin de vous, demain j'ai un contrôle ! Ce que j'ai mis : 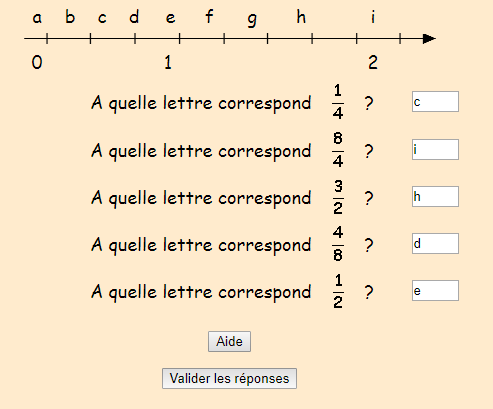  |
| « Censeur » 1544556480000
| 0 | ||
| Ce serait pas plutôt b i g c c ? Ne te base pas forcément sur les barres mais plus sur la distance de 0 à 1, on peut voir que b est à peu près à mi-distance entre les deux. Aussi, sache que pour certaines personnes c'est plus simples d'utiliser des chiffres decimaux que des fractions. Si c'est ton cas n'hésite pas à transformer 1/4 en 0,25 etc... Et même si tu préfères les fractions, essaye de voir si elles ne sont pas réductibles comme la deuxième et la quatrième. 4 et 8 sont tout deux divisible par 4, tu peux donc dire que 4/8=1/2 et 8/4=2/1=2 Je sais pas si j'ai été clair mais bon |
| 0 | ||
| Coucou, déjà je te remercie :), tous ce que tu as fait était correcte :o ! J'ai pas compris quelques petits 'trucs" et si tu pourrais m'éclairer sur ça, encore merci :) ! Pour la première je comprends pas trop pourquoi la réponse est b, parce que moi j'ai toujours utilisé la technique de faire une genre de petite illustration en répartissant les graduations en plusieurs parties comme on me l'a enseigné et bah moi j'ai trouvé ça pour la première : 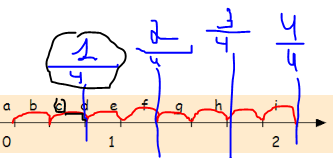 Et c'est donc pour cela que j'ai mis c et je comprends toujours pas pourquoi on met b cette fois ? J'ai tenté aussi : 1/4 = 2/8 mais ça me donne toujours c ? Pour la 3e, j'ai compris le fait que ça soit g, car on doit arrondir : 3/2 = 6/4, puis repartir cela en des parties de 4 et trouver 6 mais pourquoi ça n'a pas marché avec la première en faisant une illustration ? J'comprends pas pourquoi la 4e c'est c, car pour ça moi de base j'avais pas réfléchit, c'était logique : il y avait 8 graduations, donc j'en prends 4 des 8 et ça me fait e ? Pour la dernière j'ai mis e car j'ai fait encore une illustration pour répartir les graduations en deux parties et je me suis retrouvée avec e, je comprends pas pk c'est c ? Et aussi la moitié de 8 (comme il y a 8 graduations) c'est 4, et 4 c'est e ??? Je ne dis pas que tes réponses sont fausses, je sais que ce sont les bonnes mais c'est pas clair dans ma tête, je sais pas quand on doit diviser, quand on doit arrondir, simplifier, faire une illustration en coupant les parties ? C'est vraiment pas clair du tout dans ma tête et mm sur internet je trouve aucune leçon qui peut véritablement m'éclairer :(, mais merci et si tu pourrais encore plus m'éclairer, milles remerciements |
| « Censeur » 1544595540000
| 0 | ||
| Tu dois simplifier à chaque fois que tu peux je pense que ce sera plus simple. Par contre tes traits ne sont pas bons, tu ne dois pas les placer de 0 jusqu'au bout de la ligne( donc à 2 ) mais jusqu'à 1 et ça à chaque fois. Car quand le numérateur( chiffre du haut ) et égal au dénominateur( chiffre du bas ), par exemple 4/4, ça revient à obtenir 1 Donc comme 8/4 c'est deux fois 4/4 tu peux en déduire que c'est égal à 2 Je pense que tes erreurs viennent de cette erreur, demande moi si t'as toujours un problème |
| « Censeur » 1545165240000
| 0 | ||
| yo, j'ai besoin d'aide pour des maths : je cherche à lever l'indétermination de la limite pour x / (e^x) en +infini mais je sais pas comment faire Dernière modification le 1545165480000 |
| 0 | ||
| Théorème de croissance comparée ; e^x crois plus vite que x en gros donc ça tend vers 0 en +∞ |
| « Censeur » 1545166740000
| 0 | ||
| alors je sais mais j'ai pas le droit de l'utiliser à mon niveau puisqu'on ne l'a pas démontré :/ (terminale s) |
| 0 | ||
| Si tu as vu la limite e^x/x (qui tend vers +∞) tu peux faire la chose suivante : x/e^x = 1/(e^x/x) donc lim de 1 sur quelque chose qui tend vers +∞ ce qui donne bien 0. |
| « Censeur » 1545236520000
| 0 | ||
| ah oui j'avais pas pensé au passage à l'inverse, merci ! |
| « Censeur » 1546191960000
| 0 | ||
| J'ai encore besoin d'aide ... Je dois montrer par récurrence que 0 <= un+1 <= un <= 1 avec la suite u0=1 et un+1=f(un)=(1+un)e^un-3 et j'arrive pas au niveau de l'hérédité |
| « Citoyen » 1546264440000
| 3 | ||
Devilyomita a dit : Voici une vision intuitive des choses, mais tu ne devrais pas avoir de souci pour rédiger ça formellement. J'étudie la suite en étudiant la fonction f(x) = (1+x)*e^(x-3). Je veux montrer que f(u_n) <= u_n pour montrer la décroissance de la suite, en m'intéressant pour cela aux valeurs possibles de u_n par rapport à f. Une représentation graphique de la fonction f superposée à la première bissectrice (b(x) = x) nous sera d'une grande aide : https://i.imgur.com/Vyx5g3J.png Il existe exactement deux intersections ici signalées en rouge, et entre ces deux points la courbe de f(x) est en dessous de la courbe de x (on a f(x) < x si et seulement x est entre les deux intersections). On peut prouver tout cela en étudiant la fonction x - f(x) qui change deux fois de signe (utiliser le TVI et étudier la dérivée de x - f(x)). Attention, on n'a pas besoin de déterminer ces intersections ! Par contre avec des approximations numériques on peut montrer que 1 est compris entre les abscisses des intersections. On peut alors montrer par récurrence que f(u_n) <= u_n, soit u_(n+1) <= u_n. Il suffit en fait de montrer que tant que u_n est entre les deux intersections, elle y reste (sachant que u0 y est de base). Le fait qu'elle reste à gauche de la deuxième intersection est évident car u_(n+1) <= u_n. Le fait qu'elle reste à droite de la première intersection peut être prouvé en utilisant le fait que f soit strictement croissante. On en déduit la décroissance de la suite (u_n), le fait qu'elle soit minorée par 0 et majorée par 1 est alors immédiat. Bonus : La suite (u_n) est alors convergente car minorée et décroissante. On voit que la première intersection est sans aucun doute la limite de la suite (u_n), car la limite l d'une suite de la forme u_(n+1) = f(u_n) vérifie toujours f(l) = l. Dernière modification le 1546265280000 |
| « Censeur » 1546445340000
| 1 | ||
| Wesh wesh ça fait longtemps que j'ai arrêté l'allemand et j'ai décidé de m'y remettre. C'est une langue qui pourrait m'aider dans mon futur et que je souhaite maîtriser. Donc étant une pauvre débutante car j'ai quasiment tout oublié, je réapprends les bases et j'ai quelques petits bugs. Je vous remercierai si vous m'aidez à me rafraîchir la memory. Quand est-ce que nous utilisons les articles définis der, dis et das et les articles indéfinis "ein" et "eine" ? Comment savoir si on met l'article défini ou indéfini ? Je ne comprends pas trop quand est-ce que nous utilisons l'article indéfini "einen' ? Je comprends pas l'histoire des articles et pronoms nominatifs, accusatifs, génitifs et datifs ? Quels sont leur intérêt à chacun ? (déroule) 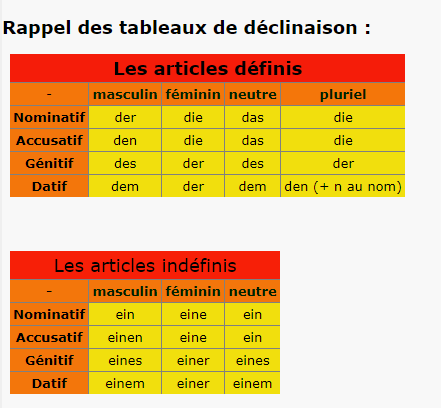 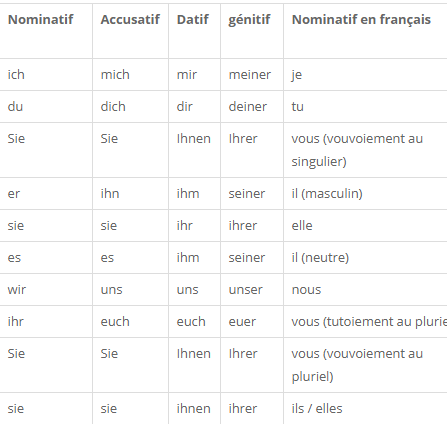 Voilà j'aurai peut-être d'autres questions juste après et si vous le voulez bien, je peux les poser en privé. Merci à vous :) ! |
| « Censeur » 1546445940000
| 2 | ||
| o mon Dieu bonne chance |
| « Censeur » 1546480020000
| 0 | ||
| Coucou ! Je suis pas une lumière en allemand mais je peux essayer de t'éclairer. Normalement dans un groupe nominal l'article et / ou (je sais plus sorry) l'adjectif s'accordent en fonction de la place de celui-ci dans ta phrase. Donc: - Nominatif: quand ton gn nominal est sujet - Accusatif: ton gn est COD -Datif : ton gn est COI ou COS -Genitif: là c'est plus spécial, ça va être utilisé quand tu vas avoir un truc type "le fils du père" il me semble Pour si tu utilises un article défini ou indéfini tu fais comme en français Sinon tu peux trouver des sites sur internet qui peuvent t'aider probablement plus que moi ou sinon perso j'avais fait l'acquisition du livre L'allemand de A à Z que j'avais trouvé assez complet |



























 Atelier 801
Atelier 801 Atelier 801
Atelier 801 
 Woowy
Woowy