| [Soutien scolaire] Aide aux devoirs |
| « Censeur » 1546614660000
| 0 | ||
| Merci je comprends désormais un peu mieux les articles ;) |
| « Censeur » 1547077020000
| 0 | ||
| L'industrie a révolutionné la société occidentale car tout va plus vite, la production est enchainée, avant les révolutions industrielles, y'a besoin de plusavoir e main d'oeuvre pour labourer un hectare de champs alors que progressivement il va y avoir besoin de moins de personnes et ça va aller plus vite avec les progrès techniques . Les premières locomotives apparaissent du coup les gens voyagent plus vite et on peut transporter des marchandises qui périment facilement genre des fleurs plus rapidement pour de grandes distances. Bon faut que tu rédiges et que tu donnes d'autres exemples, insistes bien sûr la rapidité qu'il n'y avait pas avant. |
| « Citoyen » 1547994180000
| 0 | ||
| Heyy, es-que une personne sympathique peut m'aider pour deux exos en maths, ou au moins le premier parce-que j'y comprends rien (c pr demain)  |
| « Censeur » 1547994480000
| 0 | ||
Riwell a dit : Heu... heu... Bah en fait, j'hésite entre plusieurs bonnes réponses. :/ |
| « Citoyen » 1547994720000
| 0 | ||
Aureus a dit : Cet-à-dire ? |
| « Censeur » 1547995800000
| 0 | ||
| Non vaut mieux pas, j'avais 0 de moyenne en maths. |
| 3 | ||
| Hello, pour l'exercice 1 : 1 & 2) Le plus simple est de développer les expressions qui te sont données pour arriver à l'équation de départ : f(x) = (x-5)(x-1) = x²-5x-x+5 = x²-6x+5 => C'est bien l'expression qui t'es donnée dans l'énoncé. f(x) = (x-3)²-4 = x²-6x+9-4 = x²-6x+5 => Encore une fois on retombe sur l'expression de départ Une autre méthode (je ne sais pas si vous l'avez vu ?) serait de calculer les racines de x²-6x+5 avec Δ. On a Δ=36-20=16 Donc x1=[(-6+4)/2] = 5 et x2=[(-6-4)/2] = 1. Ensuite tu factorises par les racines ce qui te donnes bien l'expression de 1) c'est-à-dire (x-1)(x-5) 3) Là, la difficulté réside à reconnaître la forme "la plus simple" pour calculer rapidement : Pour f(1) le mieux est d'utiliser (x-5)(x-1) car f(1) = (1-5)(1-1) la deuxième somme est égale à 0 donc le produit est égal à 0. f(1)=0 Pour f(3) le mieux est d'utiliser (x-3)²-4 car f(3) = (3-3)²-4 donc on a 0²-4 ce qui donne -4. f(3)=-4 Pour f(sqrt(2)) le mieux est d'utiliser x²-6x+5 car f(sqrt(2)) = (sqrt(2))²-6(sqrt(2))+5= 2+5-sqrt(2)) = 7+sqrt(2) 4) Là il suffit de résoudre les équations : (j'ai juste mis > au lieu de >= car c'est plus simple à lire mais la méthode reste la même) f(x)>0 signifie qu'il nous faut (x-3)²-4>0 Or (x-3)² toujours positif car c'est un carré donc (x-3)²>4 ce qui donne (x-3)>2 OU (x-3)<-2 et donc x>5 OU x<1. La solution est ]-∞;1] U [5;+∞[ Pour f(x)=-4 on utilise la même forme c'est-à-dire (x-3)²-4=-4. Donc on cherche (x-3)² = 0 et comme vu dans 3) l'unique solution à (x-3)²=0 est x=-3. Donc f(x)=-4 pour x=-3 Demande moi en MP (j'aurai plus de chance de le voir) si tu veux de l'aide pour le 2ème exercice. Dernière modification le 1547996820000 |
| « Citoyen » 1547997420000
| 0 | ||
Aureus a dit : Ah mdr Katow a dit : Mercii beaucoupp Katow!! J'vais pas te déranger plus avec le 2ème exo, ça va te saouler ducoup merciiii |
| « Censeur » 1547997600000
| 0 | ||
| Ah en fait j'avais trouver les bons résultats! |
| « Consul » 1548001860000
| 0 | ||
Katow a dit : Pas en seconde le discriminant. D'ailleurs, je ne conseille pas de l’utiliser en seconde, même si on a de l'avance, car certains l'avaient fait en seconde et s'étaient fait... engueuler. |
| « Censeur » 1548099000000
| 0 | ||
Nightingale a dit : Moi je me suis fait engueulé quand, en comparant deux limites de deux fonctions j'ai dit "Bah c'est évident que x^2 grandit plus vite que -x..." En fait on a pas le droit d'utiliser des propriétés si on ne les a jamais démontrées, au moins dans le cours |
| « Censeur » 1550275260000
| 0 | ||
| Ohayo ! Dans le cadre de mes TPE je dois faire un magazine scientifique (je suis en 1ere S). Je suis actuellement à la recherche-panique d'un site gratuit qui permet de faire un beau magazine complet. Je suis preneuse de toute idée ! Et merci d'avance ~ |
| 1 | ||
Maraisbbl a dit : https://www.flipsnack.com/fr/digital-magazine https://madmagz.com/fr |
| 0 | ||
Riwell a dit : Pour l'exo 2 question 3 Oups mon erreur S = [-10;1[U]1;11/3[ S = [-10;11/3[ Ptdr jviens de voir le "pour demain" et la date du post. Dernière modification le 1550353380000 |
| 0 | ||
| je dp mais tant pis qqn peut m'aider sur juste la question 2 svp? (term S)  |
| « Censeur » 1550789880000
| 0 | ||
Ski a dit : Thanks a lot ~~~ |
| « Censeur » 1550904420000
| 0 | ||
| Pour montrer que le satellite a un mouvement uniforme, tu dois d'abord dire que la seule force s'exerçant sur le satellite est l'attraction jupiterienne. Par conséquent tu peux appliquer la seconde loi de Newton qui te dit que la somme des forces est égale au produit de la masse du satellite et de son accélération. L'accélération est donc égale au quotient de la force qu'exerce Jupiter sur le satellite et de la masse du satellite. Ensuite, puisque le mouvement du satellite est circulaire, le vecteur accélération est dirigé vers le centre de Jupiter, donc dans le repère de Frenet il y a une accélération tangentielle nulle et une accélération normale égale à la valeur de l'attraction tout court (qui est égale au quotient de la force exercée et de la masse, soit (G*masseJupiter)/r^2). Puisque l'accélération normale est aussi égale à v^2/r, on a : v^2/r = (G*masseJupiter)/r^2 v^2 = (G*masseJupiter)/r v = sqrt((G*masseJupiter)/r) Tu peux aussi dire que la vitesse est constante puisque faire la primitive de l'accélération tangentielle donne une valeur constante. Dernière modification le 1550904480000 |
| « Citoyen » 1552049520000
| 1 | ||
| Helloo! J'aurai besoin d'aide pour un DM de maths qui est pour lundi car je suis pourri, je ne comprends rien donc si quelqu'un pourrait m'aider ça serait super! Mercii 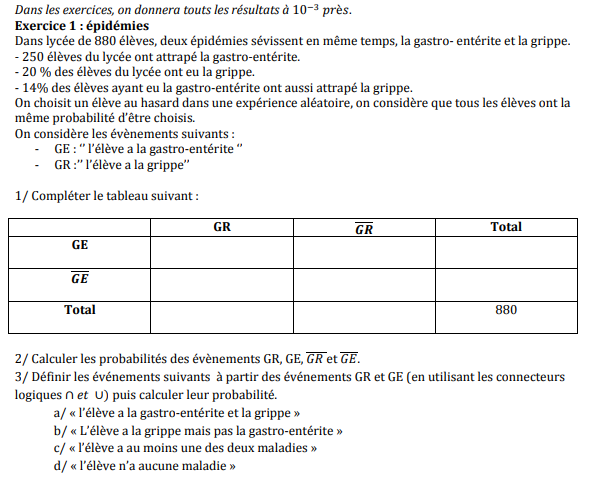 |
| 2 | ||
| 1/ Je t'ai complété le tableau avec les données qui sont données dans l'énoncé, et après je t'ai mit les calculs à faire par logique, je te laisse les faire ils ne sont pas très compliqués normalement ! Pour essayer de t'expliquer comment faire : - La première info nous dit que 250 ont la gastro-entérite donc Total de GE = 250. - La deuxième info nous dit que 20% des élèves du lycée ont eu la grippe. Or on sait qu'il y a 880 élèves dans le lycée. Donc Total GR = 20% de 880. - La dernière info nous nous que 14% de ceux qui ont la gastro-entérite ont aussi eu la grippe. Donc GE U GR = 14% de Total GE. Donc là ton tableau commence déjà à se remplir. Ensuite tu peux facilement faire des additions et soustractions en sachant que chaque case Total doit être égal à la somme de sa ligne (ou de sa colonne). Le fameux tableau
2/ Après pour calculer les probabilités qui te sont demandé la technique est similaire pour toute donc je vais juste te donner la méthode du premier : - Pour calculer P(GR), trouve la valeur qui correspond à GR dans ton tableau (nombre d'élèves qui ont la grippe au lycée) et après tu divises ce nombre total d'élèves (880). A chaque fois tu dois faire la même chose, trouver la valeur correspondant à l'évènement(tous les évènements sont dans le tableau) et puis le diviser par le nombre total d'élèves, 3/ Prenons deux évènements A et B : - U représente l'union de deux évènements : AUB signifie que qu'on prend tous les élèves qui remplissent les conditions de l'évènement A et tous les élèves qui remplissent les conditions de l'évènement B. - ⋂ représente l'intersection de deux évènements : A⋂B signifie qu'on ne prend que les élèves qui remplissent à la fois la condition de l'évènement A et de l'évènement B. A partir de ces infos tu devrais pouvoir t'en sortir. Je ne t'ai pas donné tous les résultats parce que l'important c'est que tu comprennes comment faire, donc essayes déjà avec ça et si tu n'y arrives ou que tu ne comprends pas n'hésite pas à revenir demander. |
| « Citoyen » 1552055700000
| 1 | ||
| Merci vraiment Katow, tu m'as beaucoup aidé et j'ai mieux compris ! |



























 Atelier 801
Atelier 801 Atelier 801
Atelier 801 
 Compositrice
Compositrice